Angle Between Dodecahedron Faces

Purpose

Many game programs need spherical worlds. How can a grid be put on a spherical world? The HexGridIcosahedron is one solution.

In order to calculate the errors inherent in the HexGridIcosahedron, we need to know the arc-length of each edge of the icosahedron. This arc-length equals the AngleBetweenDodecahedronFaces.

The CrossProductExample page solves this problem using CrossProducts. That solution is long and complex. A simpler solution is given below.

The Left Pentagon -- A

 Let's set up a temporary coordinate system (for this page only),
 just for finding the arc-length of an icosahedron edge.

 Let s = length of a dodecahedron edge.
 Place 3 corners of a pentagon COAED at:
 (xC=0,           yC=s,           zC=0)
 (xO=0,           yO=0,           zO=0)
 (xA=-s*cos(18°), yA=-s*sin(18°), zA=0)
 These 3 points are on the left pentagon
 in the illustration below.

The Right Pentagon -- B (when flat)

 Place 3 corners of a pentagon OCFGB at:
 (xC=0,           yC=s,           zC=0)
 (xO=0,           yO=0,           zO=0)
 (xB= s*cos(18°), yB=-s*sin(18°), zB=0) (When flat on table)
 These 3 points are on the right pentagon
 in the illustration below, 
 when it starts out flat on the table.

The Right Pentagon -- B (when rotated into place)

 Rotate the right pentagon about the y-axis (edge OC),
 until the top view of angle COB bisects angle COA.
 (It has to, because there is a similar pentagon
  touching OA that is being rotated up the same amount,
  so that all three pentagons touch each other.)
 These 3 corners of OCFGB are now at:
 (xC=0,           yC=s,           zC=0)
 (xO=0,           yO=0,           zO=0)
 (xB= s*cos(18°)*cos(crow), yB=-s*sin(18°), zB=s*cos(18°)*sin(crow)) (In 3-D)

The solution

 Where crow = elevation of pentagon OCFGB above the x-y plane
            = angle between faces of the dodecahedron
              measured at the center of the dodecahedron
            = arc-length of an edge of an icosahedron
              measured along the surface of a unit sphere.

 Because the top view of angle COB bisects angle COA,
 tan(-36°) =  (yB - yO)  / (xB - xO)
           = -s*sin(18°) / (s*cos(18°)*cos(crow))
 tan( 36°) =    sin(18°) /    cos(18°)/cos(crow)
           =    tan(18°) /             cos(crow)
 cos(crow) =    tan(18°) / tan(36°)
     crow  = arccos(tan(18°)/tan(36°))
           ~ 63.435°
           ~  1.10715 rad

The CrossProductExample also illustrates how general techniques can give exceedingly long and complex calculations, whereas a little thought can reduce the calculation required to almost zero.

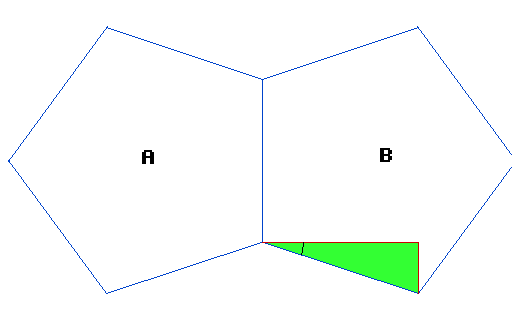
Imagine pentagon A is flat on the table. The marked angle in the green triangle is clearly 18 degrees. As you fold up pentagon B that angle (in vertical projection) will increase. You need to make it 36 degrees, and a small amount of trigonometry shows that it is accomplished when the angle made with the table is arccos(tan(18°)/tan(36°)), as above.

A colleague has just commented that this solution is less "worked out" than the CrossProductExample, so I drew two diagrams and he said "Hmm, it is obvious, isn't it."

Another fairly short solution involves inscribing a cube in the dodecahedron. This solution is exact, and should match the answer above.

This solution gives

 crow = 180° - arcsin(sin(54°)/cos(18°))
      ~  63.435°

This angle is arctan(2). Is there a simple construction which leads directly to arctan(2)? -- vk